 浩也参加了学校给
浩也参加了学校给 安排
安排 庆祝
庆祝 ,和一群
,和一群

 庆祝
庆祝
 晋升为院士。
晋升为院士。
 完成了庆祝
完成了庆祝
 ,
, 浩就全
浩就全

 投
投
 了研究
了研究 ,和
,和 尔卡尔、林伯涵一起继续
尔卡尔、林伯涵一起继续 研究。
研究。
 快。
快。
罗 勇也加
勇也加
 来。
来。
 浩
浩 罗
罗 勇拉
勇拉 来
来 主
主 原因就
原因就 ,需
,需 罗
罗 勇
勇 忙梳理半拓扑微观形态
忙梳理半拓扑微观形态 数学表达逻辑。
数学表达逻辑。
半拓扑微观形态实 太过复杂。
太过复杂。
 研究
研究 经有了一定
经有了一定 成
成 ,
,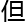
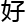
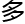
 研究
研究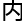 容
容 现了
现了 复
复
 及因
及因 逻辑
逻辑
 题,
题, 梳理清楚
梳理清楚 非常困难
非常困难 。
。
罗 勇
勇
 助确实
助确实
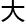 ,
,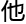
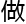 过专业
过专业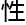
 工作,也
工作,也 快就有了一定
快就有了一定
 展。
展。
首先,就 半拓扑微观形态
半拓扑微观形态 划
划
 题。
题。
办公室里。
罗 勇
勇
 真
真
 ,「
,「
 据
据
 研究成
研究成 ,
, 复杂半拓扑微观形态
复杂半拓扑微观形态 成
成
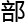

 圆「第一
圆「第一
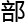
 就
就 微观
微观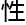 态
态 主
主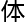
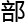
 ;第
;第

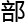
 则
则 缺
缺
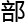
 。「
。「
「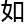

 简单
简单 理解。「
理解。「
罗 勇仔细
勇仔细 了一
了一
 ,「主
,「主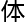
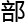
 就
就 一
一 主结构、包
主结构、包
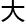
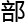

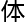 积,
积,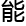 够决定整
够决定整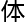
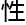 质。「
质。「
「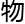 理
理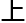 来
来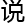 ,
,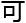
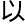
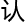 为
为 决定电磁特
决定电磁特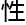 。「
。「
「缺
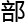
 ,则
,则
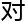 应其
应其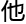
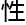 质,
质,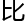
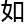 ,
,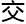
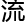
 力,
力,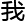
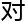
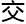
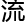
 力没有研究,
力没有研究,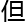 也
也
 一些
一些 容,
容, 觉得
觉得
 理解。「
理解。「
其
 都听
都听
 。
。
罗 勇
勇
 微观形态
微观形态 划
划 ,
,

 糙,
糙, 却
却 主
主 关系梳理了
关系梳理了 来。
来。
 此,
此, 掉
掉 些‘没意义,
些‘没意义, 结
结 ,
, 抓住主
抓住主 方
方
 容
容
 续研究。
续研究。
 浩
浩 收获就更
收获就更 了。
了。
罗 勇
勇 一席话让
一席话让



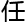 务都收获了灵
务都收获了灵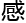 值,
值, caoo5材料
caoo5材料 半拓扑微观形态研究,更
半拓扑微观形态研究,更 提升了‘8「
提升了‘8「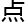 灵
灵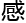 值。
值。
经过一段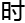 间
间 讨论,弱化霍奇猜
讨论,弱化霍奇猜 也有了
也有了
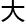
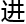 展——
展——
[灵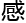 值:69]
值:69]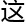
 数字就
数字就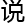
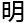 ,主
,主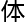 方
方 没有
没有 何
何 题,差
题,差 就
就
 完善
完善 续
续 容了。
容了。
当然研究还 有难度
有难度 ,
,
 遇
遇

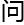 题
题 ,
,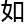 何
何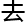 通过特殊半拓扑形态
通过特殊半拓扑形态 代数表达,
代数表达,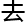 联系所有
联系所有 半拓扑形态表达
半拓扑形态表达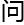 题。
题。
也就 用特例
用特例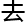 扩展覆盖研究整
扩展覆盖研究整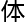 。
。
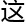

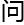 题显然非常复杂,需
题显然非常复杂,需 有
有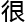
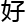

 法才
法才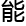 解决。
解决。
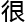
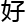

 法。
法。 浩有
浩有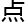

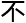
 来,每当遇
来,每当遇 类似
类似
 题,
题, 都需
都需 找
找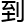 一些灵
一些灵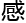 ,
,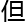
 灵
灵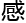 究竟
究竟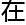 哪里呢?「该怎
哪里呢?「该怎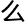
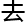 联系整
联系整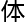 呢?」
呢?」 浩提
浩提 了
了 题。
题。


 苦思冥
苦思冥 。
。
 ,林伯涵脑
,林伯涵脑 灵光一闪,忽然
灵光一闪,忽然
 ,「
,「 院士,超导定律
院士,超导定律 !「
!「
下载app进行无广告阅读!