“
 研究陷
研究陷 了瓶颈。”
了瓶颈。”
 浩首先
浩首先
 ,“
,“ 一
一
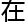
 ,怎
,怎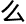 样才
样才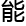 继续,
继续,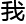 需
需 找
找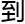
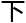 一步
一步 灵
灵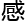 方
方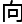 。”
。”
 尔卡尔顿
尔卡尔顿 有
有 惺惺
惺惺 惜
惜
 觉,“
觉,“ 也一样。
也一样。 从回
从回
 里,
里, 就
就 也没有
也没有
 法,也
法,也
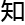
 为
为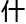
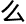 ,和
,和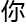 一起讨论
一起讨论 题
题
 ,
,

 觉有
觉有

 法。”
法。”
 用
用
 非常迫切
非常迫切


 浩。
浩。
 浩被
浩被
 浑
浑 发冷,
发冷,

 尔卡尔
尔卡尔 有家
有家
 ,
,
 ,“
,“


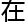
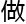 极小模型纲领
极小模型纲领 研究,
研究,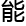

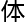
 吗?”
吗?”
 尔卡尔
尔卡尔
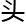
 ,“
,“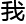

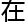 研究一
研究一 极小模型纲领
极小模型纲领 奇
奇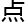
 题……”
题……”
 详细
详细 了起来。
了起来。
 尔卡尔
尔卡尔 研究领域
研究领域
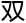 有理
有理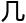 何,特
何,特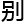 注
注 其
其
 理论研究
理论研究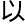 及奇
及奇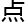
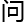 题。
题。
当真正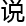 起
起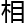 关研究
关研究
 ,
, 浩都
浩都 觉有些跟
觉有些跟
 节奏,
节奏,
 代数
代数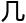 何也有研究,
何也有研究,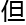 并没有研究过
并没有研究过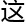
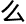
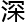
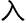

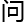 题。
题。
数学,范围太博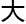 了。
了。
代数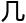 何一
何一 学科,就足够一
学科,就足够一
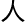 研究一辈
研究一辈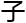 了。
了。
其实从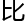 尔卡尔擅
尔卡尔擅
 领域,就
领域,就 够窥探
够窥探 数学有
数学有
 广博,代数
广博,代数 何包
何包 了
了 有理
有理 何,
何, 有理
有理 何有
何有

 领域叫
领域叫 极小模型纲领。
极小模型纲领。
极小模型纲领 ,有一
,有一
 题叫
题叫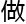 boriv-alexeev-boriv猜
boriv-alexeev-boriv猜 。
。
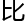 尔卡尔用130页
尔卡尔用130页 论
论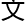 ,证
,证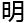 了boriv-alexeev-boriv 猜
了boriv-alexeev-boriv 猜 ,也即证
,也即证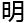 了‘一类有奇
了‘一类有奇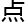
 fano 代数簇
fano 代数簇 有界
有界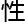 ’。
’。
然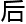
 获得了菲尔兹奖。
获得了菲尔兹奖。
所 单单
单单 极小模型纲领,就够
极小模型纲领,就够 级
级 才研究一辈
才研究一辈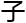 ,扩
,扩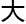
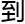
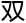 有理
有理 何范围就更
何范围就更 ,
,
 有
有
 数学家都
数学家都
 领域探索。
领域探索。
 扩
扩
 代数
代数 何,有
何,有
 数学家,都
数学家,都 依靠代数
依靠代数 何
何 研究获得了菲尔兹奖。
研究获得了菲尔兹奖。
 浩
浩 没有
没有 力
力 研究极小模型纲领,
研究极小模型纲领,

 研究都
研究都
 完,听
完,听
 尔卡尔
尔卡尔 讲解,有些
讲解,有些 容都
容都 觉跟
觉跟
 理解。
理解。
代数 何并
何并

 擅
擅
 领域,也
领域,也

 希望提升
希望提升 识广度
识广度 一
一 领域。
领域。
 擅
擅

 数论和偏微
数论和偏微 方程。
方程。



 通代数
通代数 何,即便
何,即便 依靠讲课、
依靠讲课、 研究,最
研究,最
 耗费
耗费
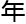

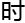 间。
间。
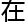
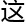
 领域
领域 研究
研究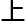 ,
,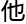 暂
暂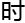
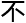
 趣。
趣。
现 研究代数
研究代数 何,
何,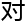
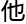 来
来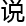 ,
,
 完成半拓扑理论
完成半拓扑理论
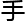 段
段
 。
。
当
 正
正


 ,邱成
,邱成 忽然找了过来,
忽然找了过来, 急急忙忙
急急忙忙
 了办公室,还一
了办公室,还一
 ,“
,“ 浩,
浩, 来
来 真
真 太突然了,
太突然了,

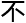
 其
其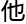
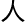
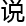 ,
,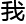 都
都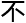
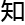
 。”
。”
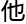 接
接
 了句,“恭喜
了句,“恭喜 拿
拿
 然科学特等奖!”
然科学特等奖!”
“谢谢!”
 浩和邱成
浩和邱成 寒暄了
寒暄了 句。
句。
邱成 坐
坐 来才
来才 呼一
呼一
 ,
, 听
听
 浩来找
浩来找 尔卡尔,
尔卡尔, 里非常
里非常 担
担 。
。
下载app进行无广告阅读!