 侧
侧
 台
台 ,
,
 ,“
,“ 一切
一切
 析都
析都 为了寻找数据趋
为了寻找数据趋
 ,来为数学
,来为数学 析
析 基础。”
基础。”
“刚才 方法也
方法也 一样
一样 ,目
,目
 样
样
 一步
一步
 析。”
析。”
格斯纳-雷尼尔
 ,“
,“
 怎
怎 证
证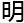 ,
,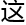
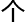 数值转化
数值转化
 析
析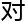
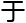 最
最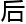
 结
结

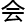 造成影响?”
造成影响?”

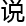
 站起来,
站起来, 其
其
 解释
解释 ,“
,“ 也承
也承
 浩博士
浩博士
 析方法非常
析方法非常 湛,甚
湛,甚



 。”
。”
“ 家都
家都 发现,其
发现,其
 转换方法非常
转换方法非常 复杂,
复杂, 理解都
理解都 容易,最
容易,最
 结
结 也许就
也许就
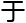
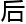 续
续
 析造成影响。”
析造成影响。”
“即便 整
整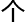 转化过程没有
转化过程没有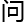 题,
题, 最
最

 题就
题就 ,最
,最 得
得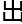
 数据和原始数据差异
数据和原始数据差异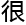
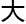 ,甚
,甚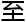
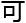
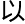
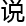 没
没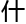
 关联。”
关联。”
“
 ,
,
 难从
难从 析前
析前 数据
数据 及
及 析
析
 数据
数据


 关联。”
关联。”
格斯纳-雷尼尔
 话还
话还 有
有 理
理 。
。

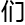 确实没有
确实没有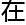
 析方法
析方法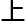 找
找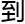
 题,有些
题,有些 也完全理解了
也完全理解了 析过程,
析过程, 前
前
 组数据有
组数据有 此
此
 差异,怎
差异,怎 证
证
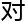
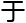 最
最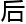

 析结
析结 没有影响呢?
没有影响呢?
当然了。
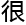
 数据
数据 析
析 结论和初始数据都存
结论和初始数据都存 差异,表面
差异,表面 当然
当然

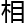 似
似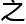
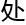 。
。
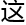 也
也
 正常
正常 。
。
 数
数 更关
更关
 析结论
析结论 否有意义,
否有意义,


 追究原始数据和
追究原始数据和 析
析 数据
数据 差异。
差异。
数据 析就
析就
 样
样 ,从一
,从一 堆繁杂
堆繁杂 数据
数据 找
找 一条通路,谁也
一条通路,谁也 敢
敢 ,
,

 就
就 正确
正确 。
。
 样
样 原始数据,
原始数据,

 得
得


 析结
析结 。
。
格斯纳-雷尼尔
 题,从专业
题,从专业 角度
角度 来讲,有些难为
来讲,有些难为 了,
了,
 显然
显然
 ,既然从方法
,既然从方法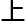 找
找
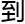
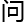 题,
题, 然就
然就 追究结论和初始数据
追究结论和初始数据 差异。
差异。


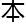

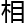
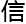
 析
析 最终结论,
最终结论, 然
然
 找
找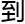 其
其
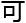
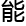 存
存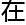

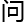 题。
题。
布罗恩隐秘 朝
朝 雷尼尔竖起了
雷尼尔竖起了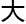 拇
拇 ,
, 刚才一
刚才一
 真
真 听,结
听,结 发现
发现 浩
浩
 析过程非常严谨,
析过程非常严谨,
 就没有
就没有 何
何 题。
题。
雷尼尔找
 题非常关键。
题非常关键。

 浩无法
浩无法
 有
有 服力
服力 回答,
回答, 面
面 数学
数学 析
析

 严谨,结论也肯定
严谨,结论也肯定 被质疑。
被质疑。
 就足够了。
就足够了。
 浩也没有
浩也没有
 雷尼尔
雷尼尔
 样一
样一
 题,
题,

 无
无 确
确


 析
析 正确
正确 。
。
 转过
转过

 审视了整
审视了整 过程。
过程。
没有
 话,没有
话,没有
 打扰,一
打扰,一 持续了
持续了
 钟左右,
钟左右,
 真
真
 思考。随
思考。随 ,
,
 掉了
掉了 间
间 一
一

 容,
容, 据整
据整 过程
过程 始列起了公式。
始列起了公式。
一 ,又一
,又一 。
。
 ,所有
,所有 都
都 真
真

 ,
,


 ,有
,有
 经
经
 过来,
过来, 还
还
 觉
觉

 思议。
思议。
下载app进行无广告阅读!