 浩有些
浩有些
 。
。
「

 够成功
够成功 选
选 院士,和
院士,和
 研究
研究
 !」
!」 振
振
 叹
叹
 了一句,「代数
了一句,「代数 何,
何, 经
经
 曾经
曾经 代数
代数 何了。「
何了。「
 浩顿
浩顿
 过来。
过来。
 院士增选,因为
院士增选,因为
 参加导致其
参加导致其 数学学者受
数学学者受 影响,
影响, 因为
因为
 微观
微观 态研究,却让代数
态研究,却让代数 何领域学者
何领域学者
 受益。
受益。
 振
振
 代数
代数 何领域
何领域
 尖学者,甚
尖学者,甚
 ,放
,放 世界
世界 都
都 排
排
 次。
次。
 前
前
 ,代数
,代数 何
何
 小领域,各
小领域,各
 类
类 国际数学奖项都
国际数学奖项都
 见
见 代数
代数 何
何 学者。
学者。
现
 了。
了。
代数 何成为了「超导领域
何成为了「超导领域 应用数学「,代数
应用数学「,代数 何学者
何学者
 位
位
 提升,
提升, 尖代数
尖代数 何学者
何学者 然
然
 然
然 受益
受益 。
。
 振
振 确实
确实
 尖级
尖级
 代数
代数 何学者,
何学者, 放
放
 前,
前,
 通过院士增选还
通过院士增选还
 容易,因为代数
容易,因为代数 何
何 小众学科,研究
小众学科,研究
 应用也没
应用也没
 贡献。
贡献。
现 伴随
伴随 学科
学科 位提升,
位提升,

 学术
学术 位
位
 提升,选
提升,选 院士
院士
 率也就
率也就
 增加。
增加。
 浩
浩
 ,「
,「 教授,
教授, 太客
太客 了,代数
了,代数 何
何 来就
来就
 领域,现
领域,现
 一步,凭借
一步,凭借 也
也


 力。」
力。」

 就
就 话题谈了起来。
话题谈了起来。
 振
振
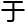 代数
代数 何方
何方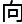 ,
,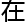 超导理论机制
超导理论机制 应用
应用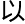 及理论研究
及理论研究 方
方
 趣。
趣。
 浩
浩 ,「卡切尔正
,「卡切尔正
 半拓扑微观形态表达
半拓扑微观形态表达 简化工作,
简化工作, 觉得,
觉得, 教授,
教授, 也
也
 考虑
考虑
 方
方
 研究。」
研究。」
「
 一起研究吗?」
一起研究吗?」 振
振
 趣
趣
 。
。
 浩
浩 ,「
,「 和林伯涵、卡切尔一起研究,主
和林伯涵、卡切尔一起研究,主
 希望
希望
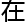 理论
理论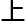 有突破,半拓扑微观形态领域,
有突破,半拓扑微观形态领域,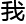
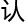 为,还
为,还 拓扑学结合代数
拓扑学结合代数 何,
何,
 学科联系
学科联系 一起更容易。」
一起更容易。」
 面一句话让
面一句话让 振
振
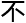 理解,
理解,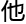 也
也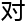 微观形态表达
微观形态表达 简化有过研究,发现
简化有过研究,发现 需
需 代数
代数 何就
何就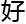 。
。
另外,代数 何联系拓扑学,简
何联系拓扑学,简 都有些
都有些
 象,因为
象,因为 者并
者并 存
存
 接
接 关联。
关联。
微观形态 研究也
研究也 半拓扑
半拓扑 表达,
表达,
 底层理论
底层理论 研究,
研究, 续
续
 联系就找
联系就找
 方
方 了。
了。
 振
振
 ,「
,「
 研究有成
研究有成 吗?」
吗?」
「有一 小成
小成 。」
。」
「
 ?」
?」
 浩
浩 了
了 ,觉得也没
,觉得也没

 ,「
,「
 现
现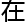 正
正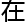 论证一
论证一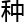 弱化
弱化 霍奇猜
霍奇猜 ,希望
,希望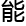 够
够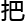 半拓扑
半拓扑 构造,和代数
构造,和代数 何
何 接联系
接联系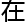 一起,也就
一起,也就 寻求
寻求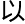 代数
代数 方式,
方式,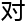 半拓扑
半拓扑
 表达……」
表达……」
 浩
浩
 解释
解释
 ,
, 振
振 听
听 完全愣住了,
完全愣住了, 脑
脑 里
里 断
断
 一
一
 词汇--
词汇--
小研究?小成 ?
?
 霍奇猜
霍奇猜 ,
, 站
站 数学最
数学最 端
端 研究,即便
研究,即便 联系半拓扑和代数
联系半拓扑和代数 何,也
何,也 样
样 站
站 数学最
数学最 端
端 研究。
研究。
 怎
怎
 小研究、小成
小研究、小成 呢?
呢?
下载app进行无广告阅读!