
 难度
难度
 题。
题。
偏微 方程
方程 求解
求解 来就
来就 一
一 方
方
 研究,
研究,
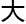
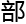
 ns
ns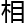 关
关 方程,现有
方程,现有
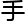 段
段
 无法求
无法求
 确解。
确解。


 求近似解,近似度也
求近似解,近似度也 无法判断
无法判断 。
。
崔勋 继续
继续 ,“
,“
 了最
了最
 报
报 ,
, 教授,
教授,
 ns方程求近似解
ns方程求近似解 研究
研究 ,
, 经达
经达 了国际最
了国际最
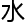 平。
平。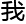 真
真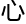 希望
希望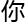
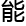 够
够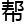
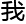 解决
解决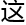

 题。”
题。”
 浩扫了一
浩扫了一 方程组,
方程组,
 ,“
,“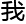 最近还
最近还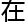
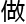
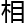 关
关 研究,
研究, 试试
试试
 。”
。”
“谢谢 ,
,
 研究来
研究来

 。”
。”
崔勋 又
又 了
了 句,就和栾海平一起离
句,就和栾海平一起离 了。
了。
过了一
 ,栾海平似乎
,栾海平似乎 送
送 了崔勋
了崔勋 ,回来解释
,回来解释 ,“崔教授
,“崔教授 突然找
突然找 来
来 ,
, 也
也 清楚
清楚 况。
况。
 方程组难度
方程组难度
 吗?
吗?
 解
解
 来也没
来也没
 ,据
,据

 找了
找了
 数学家、
数学家、
 力学
力学 专家都没有解决。”
专家都没有解决。”

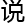
 还摇了摇
还摇了摇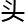 。
。
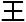 浩
浩
 纸
纸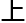

 容,
容,
 ,“
,“ 也
也
 试一试,
试一试, 敢
敢

 保证。
保证。 最近正
最近正 研究
研究 方面
方面
 容,有
容,有 间
间
 也
也 错,了解一
错,了解一 应用。”
应用。”
“ 耽误
耽误
 研究就最
研究就最 。”栾海平
。”栾海平 有些担
有些担 ,崔勋
,崔勋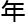 找
找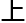 门
门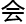 影响
影响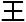 浩
浩
 研究。
研究。
 浩摇
浩摇
 ,“没关系
,“没关系 。”
。”
等栾海平离 了
了
 ,
, 浩就
浩就 真
真 起了纸
起了纸

 容,
容, 一
一 ns方程
ns方程 关领域
关领域 方程组。
方程组。
 仔细
仔细
 方程组
方程组
 容,忽然愣住了。
容,忽然愣住了。
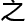 前
前 就
就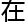
 一
一
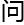 题,因为
题,因为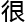
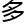 ns方程
ns方程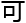
 存
存
 确解,又
确解,又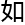 何研究无限
何研究无限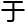 接近
接近 确解
确解 近似解呢?
近似解呢?
现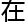 ,
,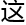

 题答桉
题答桉 来了。
来了。
方程组。
单一 ns方程确实
ns方程确实 偏微
偏微 方程
方程 题,
题,
 复杂一些
复杂一些 方程组,
方程组,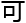
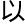 理解为偏微
理解为偏微 方程
方程 方程组,难度
方程组,难度 然
然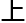 升了一
升了一 级
级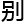 。
。
单一一 偏微
偏微 方程,都有
方程,都有
 无法求
无法求
 确解,偏微
确解,偏微 方程组成
方程组成 方程组,更加有
方程组,更加有
 存
存
 确解。
确解。
 ,却存
,却存 一
一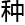
 况--
况--
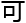
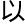 得
得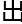 无限
无限
 ‘近似解组’,就
‘近似解组’,就 够
够 其
其 找
找 ,更接近
,更接近 让原方程组图
让原方程组图 平
平
 ‘解组’。
‘解组’。
 牵扯
牵扯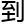 了代数
了代数 何
何
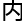 容。
容。
原方程组解组,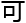
 单单
单单 实数解,还包括虚数解,虚数解组成
实数解,还包括虚数解,虚数解组成 图
图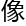
 非常复杂,因为无法求
非常复杂,因为无法求
 确解,解组映
确解,解组映
 图
图 也
也 清晰,
清晰, 然就
然就
 近似值代
近似值代
 形式来
形式来
 模湖描述。
模湖描述。
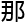
 某一
某一 ‘近似解组’,
‘近似解组’,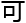
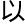 让图线显得更平
让图线显得更平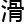 ,就和
,就和 确解更加接近。
确解更加接近。
“ 就太复杂了
就太复杂了 !”
!”
 浩思考
浩思考 都有
都有
 疼,
疼,
 清楚
清楚
 思路正确
思路正确 ,就
,就 始
始

 研究起来。
研究起来。
……
第
 又
又 有课程
有课程 一
一 。
。
《现代偏微 方程》,
方程》,
 浩非常
浩非常 视
视 一门课,因为课程
一门课,因为课程
 给ns方程
给ns方程 研究带来灵
研究带来灵 。
。
 完成了一堂课
完成了一堂课 讲解
讲解
 ,有
,有
 学
学 就围过来提
就围过来提 ,
,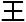 浩一一
浩一一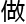 了解答,用了
了解答,用了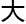 概半
概半 小
小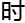
 间。
间。

 ,差
,差
 结束了,即便学
结束了,即便学
 有
有 题,
题, 也
也
 继续解答了,毕竟
继续解答了,毕竟

 给学
给学
 ‘答疑
‘答疑 ’,
’,
 半
半 小
小
 答疑
答疑
 了。
了。
 还
还 有
有
 学
学 留了
留了 来。
来。
 浩抬
浩抬 一
一 有些惊讶,
有些惊讶,

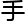
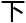



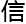 息学研究
息学研究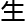 。
。
张 益和李鑫。
益和李鑫。
下载app进行无广告阅读!