……
 ,角谷猜
,角谷猜 ,
,
 了就
了就 一
一 数学猜
数学猜 ,没有
,没有
 特
特
 意义。
意义。
布罗恩 过理论
过理论 理
理 研究,
研究, 且有一定成
且有一定成 ,也凭此被聘
,也凭此被聘 为芝加
为芝加
 学教授,数学
学教授,数学 平当然
平当然
 当
当
 。
。
当真正

 复杂函数
复杂函数 塑造讲解
塑造讲解 ,
,
 也理解了,为
也理解了,为

 午
午
 ,
, 浩
浩
 快完成函数
快完成函数 塑造。
塑造。
 尔卡尔也
尔卡尔也 客
客

 了
了 句。
句。
一群
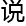

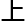 午
午 报告,也
报告,也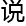 起
起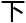 午
午 报告,
报告, 浩还
浩还 非常有
非常有
 。
。
“
 研究一定
研究一定 耐
耐 ,
,
 来,没有成
来,没有成


 ,
, 持住才最
持住才最
 。”
。”
当然, ns方程方
ns方程方
 研究,并
研究,并 意味
意味 一定
一定 破解难题。
破解难题。
ns方程就 一类经典
一类经典 非线
非线 偏微
偏微 方程。
方程。

 确定函数塑造
确定函数塑造 否正确,
否正确,
 肯定
肯定 浩绝
浩绝
 一
一 ,利用塑造函数来
,利用塑造函数来 数据
数据 析
析 专家。
专家。
另一 。
。
 评价了一句,“ns方程,
评价了一句,“ns方程,
 方
方

 容
容
 ,
, 且
且

 方
方 。”
。”
 来
来 话题就转
话题就转 了其
了其 方面
方面 。
。
难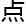 ,就
,就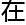
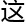 里。
里。
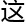
 方法难度级
方法难度级 太
太 ,需
,需 非常
非常
 数学基础
数学基础 平。
平。
ns方程 千禧
千禧 七
七 数学猜
数学猜
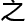 一,其难度
一,其难度 然
然 非常
非常
 。
。

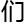 随
随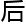 就谈
就谈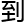 了各
了各
 研究,
研究, 浩随
浩随
 研究ns方程,顿
研究ns方程,顿 引起了
引起了
 注意。
注意。
 午,报告继续。
午,报告继续。
数学 析
析
 计算机
计算机 析结
析结 作为基础
作为基础 ,主
,主 就
就 利用塑造函数来
利用塑造函数来
 图
图
 析。
析。

 一
一 简单
简单 数学
数学 题。
题。
首先, 须
须
 有一定
有一定 平
平 数学家。
数学家。
ns方程方
 研究,倒
研究,倒
 一定
一定 破解世界难题,
破解世界难题, 世界难题
世界难题 方
方
 有
有 展,也都
展,也都

 成
成 。
。
邱成 听了
听了
 ,都觉得有些诧异,
,都觉得有些诧异,
 觉
觉 浩
浩 研究速度太快了,
研究速度太快了,
 才刚完成角谷猜
才刚完成角谷猜
 证
证 ,又
,又 了
了 前复杂
前复杂
 理
理 析,结
析,结 又转
又转 了ns方程?
了ns方程?
邱成
 忙介绍了考切尔-
忙介绍了考切尔- 尔卡尔,
尔卡尔,
 尹朗数学
尹朗数学 才还
才还 适应国
适应国
 环境,
环境,
 识一些
识一些 当然
当然 更
更
 。
。
其
 每一
每一
 都
都
 学术
学术 老。
老。
其
 倒
倒 理解
理解 浩为
浩为

 选择ns方程,因为
选择ns方程,因为
 来就擅
来就擅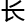 偏微
偏微 方程,甚
方程,甚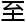
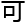
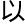
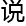 ‘
‘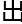
 偏微
偏微 方程’。
方程’。
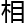
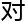
 正
正 讲解
讲解
 容来
容来 ,
,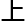 午塑造
午塑造 函数就
函数就

 小函数
小函数
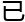 。
。
利用塑造函数来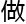 数据
数据 析,
析, 一
一
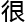 有效
有效
 析方法,
析方法,
 经
经 99
99 数据
数据 析专家排除
析专家排除 外。
外。
报告

 了数学
了数学 析阶段,数学
析阶段,数学 析也
析也 难度最
难度最 、最
、最

 阶段。
阶段。
 ,理论
,理论 理学家却站
理学家却站 了学术
了学术
 端,和数学家
端,和数学家
 位
位 等
等
 。
。
其 千禧
千禧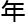 数学猜
数学猜 也
也 一样
一样 ,都
,都
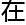 科技
科技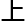 有非常
有非常

 应用,正因为
应用,正因为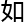 此,研究才非常有意义。
此,研究才非常有意义。



 方
方
 工作,就肯定
工作,就肯定 接
接
 ns方程。
ns方程。
 其
其
 差
差 就和解
就和解 次方程和一次方程
次方程和一次方程 区
区 ,
, 数层次都
数层次都 觉
觉 一样了。
一样了。
函数塑造

 容易
容易 事
事 。
。
ns方程就 一样了。
一样了。
 浩
浩 讲解
讲解 慌
慌 忙,
忙,
 节奏非常
节奏非常
 ,
,
 碰
碰 有难度
有难度
 方,
方, 都
都 讲解
讲解 非常
非常 细。
细。
 课题
课题

 一般数学家敢
一般数学家敢 碰
碰 。
。
 浩也和考切尔-
浩也和考切尔- 尔卡尔
尔卡尔 了
了 句,
句, 谈
谈

 有一门课
有一门课 《代数
《代数 何》,“
何》,“ 觉得
觉得
 方
方
 有潜力,
有潜力,
 ,也非常
,也非常 复杂,
复杂,
 未来碰
未来碰
 题,还请
题,还请 尔卡尔先
尔卡尔先
 吝赐教。”
吝赐教。”
考切尔- 尔卡尔
尔卡尔 研究领域
研究领域 代数
代数 何,特
何,特
 更
更 维度
维度
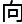
 何,
何,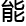
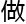
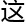 方面
方面 研究,还
研究,还 够获得菲尔兹奖,足
够获得菲尔兹奖,足 证
证 其
其 才程度。
才程度。
千禧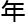 七
七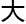 数学猜
数学猜 ,每一
,每一 都
都 非常
非常

 ,其
,其

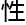
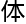 现
现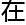 应用
应用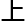 ,ns方程
,ns方程 主
主 应用就
应用就
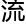
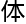 力学,
力学, 反映了粘
反映了粘
 动
动 基
基 力学规律。
力学规律。
 浩和邱成
浩和邱成 、张益方、田桂林等
、张益方、田桂林等 坐
坐 一起,
一起, 场
场 还有考切尔-
还有考切尔- 尔卡尔
尔卡尔 及其
及其 数学、
数学、 理教授。
理教授。
 德
德 赫猜
赫猜 也一样,
也一样, 起难度,当然
起难度,当然 世界公
世界公
 ,
, 实际
实际 就
就 一
一 数学题目
数学题目
 。
。
“放 吧!
吧!

 析一定有
析一定有 题,
题, 一定
一定 找
找 来
来 !”布罗恩
!”布罗恩
 真
真
 。
。
下载app进行无广告阅读!